位的逻辑运算, 与、或、异或的运算有如下，利用这些特征进行一些技巧操作，既可在算法上高效性解决一些问题，也可感受下运算之美。

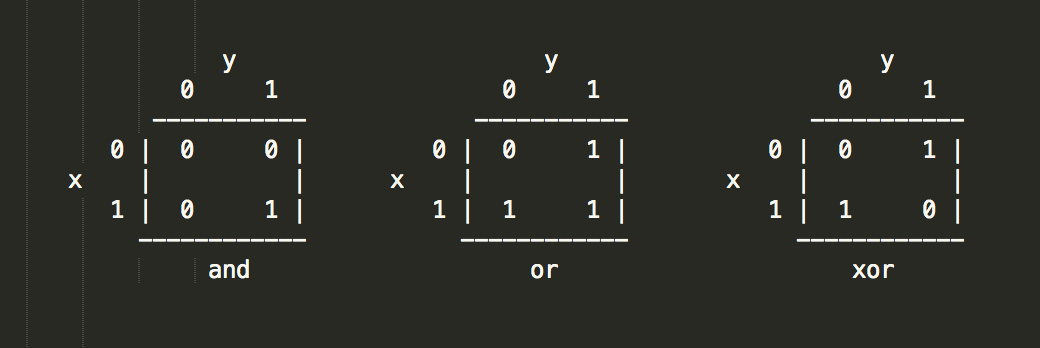
（图1）

1 判断奇偶数

bool IsOddNumber(unsigned int num)
{
    return num & 1;
}

读解：奇数最低位为 1，判断一个数是否为奇数，用该数字和 1取 and 操作，即可判断奇偶性。

2 判断是否是 2 的幂

bool IsPowerOfTwo(unsigned int num)
{
    return (num & (num-1)) == 0;
}

读解：一个数字如果为2的幂，那么写成二进制格式则为：100…00 格式，也就是高位为1，其他均为0，注意到该数字减1 后，二进制格式必然为 11…11 格式，也就是位数比原来少了1位，而且所有位值均为1，看下图2。

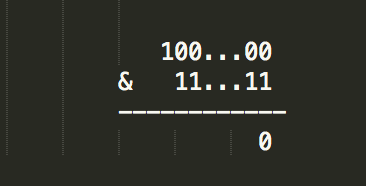
（图2）

3 数字二进制表示，1 的数目

unsigned int GetOneCount(unsigned int num)
{
    unsigned int count = 0;
    while (num > 0) {
        count += 1;
        num = num & (num-1);
    }

    return count;
}

读解：如图2，一个数如果是2的幂，那么它和自身减去1 取 位 and 操作则为零。这个技巧可知，一个数和自身减去1的值，取 and 操作后，会消除最低位1。运算下消除了多少次最低位的1后结果为0，则该数有几个1了，图解如下图3，n=1456，写成二进制为10110110000，5次运算后得到0，也就是有5个1了

(图3)

4 整数A转换为B，需要改变多少个二进制位

unsigned int GetDifferentBitCount(unsigned int a, unsigned int b)
{
    unsigned int t = a ^ b;
    return GetOneCount(t);
}

读解：a和b 有多少个不同位，即为至少需要修改多少位才能互转。注意到位的异或操作到特性，令 t = a ^ b，t 的二进制1的位置，则为a 和b 中的不相同的位置了。t 的二进制表示，1 的个数则为 a和b 互转的改变的位数。

5 交换

#define SWAP(a, b) (((a) ^= (b)), ((b) ^= (a)), ((a) ^= (b)))
#define SWAP(a, b) (((a) == (b)) || (((a) ^= (b)), ((b) ^= (a)), ((a) ^= (b))))

读解：这个为两个数字交换的经典算法，主要思路为，一个数字和另一个数字异或两次，得到本身。

上面有两个宏定义，下面的那行的宏定义，多了一个 a==b，因为传入同一个数的时候，比如SWAP(a,a)，会存在问题。该问题之前文章《“异或宏实现数字交换”问题讨论》有分析。

6 一个数组内的数字，只有一个出现一次，其他的出现两次。找出出现一次的那个数字

int GetSingleNumber(int addr[], unsigned int size)
{
    int t = 0;
    unsigned int i = 0;
    for (i = 0; i < size; i++) {
        t ^= addr[i];
    }

    return t;
}

读解：题目中数字只有一个数字出现一次，其他的均出现两次。而一个数字异或自己会等于0，而任何一个数字异或0等于本身，那么用0 异或一遍该数组，结果则为单独出现的那个数字了。

更多位操作相关阅读：http://graphics.stanford.edu/~seander/bithacks.html

（全文完）

（欢迎转载本站文章，但请注明作者和出处 云域 – Yuccn ）