(2011年写于新浪博客，今天新浪“牛皮癣”多得～～，把文章整理下，挪过来吧)

很多应用上都会用到最短路径，尤其迷宫算法中，以前写一个游戏五子连珠的时候，也用到最短路径算法。

说明一下五子连珠游戏规则：

1）（如下图）游戏开始时候，盘面中随机有几个不同颜色的珠子，游戏目标是把珠子移动到别的和它颜色相同的珠子周围，并且连成一条直线；

2）当直线上的珠子达到五个(或以上)的时候，珠子就会消除，并获得一定分数，连接珠子越多，得分越多；

3）每移动一次珠子的时候，盘面也会生成随机的颜色的几个珠子在随机的位置上；

4）当盘面的珠子满了的时候，游戏结束。

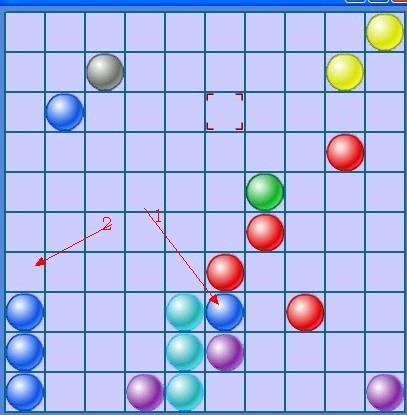
上图，目标想把蓝色珠子要从箭头1 的位置通过最短路径移动到箭头2的位置，首先要它有通路到2的位置，才有最短路径可言。

本图是有通路的，而且不止一条，现在开始分析查找一条最短路径。把位置信息用数组来表示，那么位置1就是（5,7）了，2 为（0,6）。

从1 由近到远遍历能到达的点，并且借助一个辅助数组来表示能遍历到的点需要的最近步数，这个辅助数组的大小和图中格子大小相等。开始时辅助数组初始化一个数字（如-1），表示还没有到达的点。

标记操作：

开始遍历，把点1 按上下左右的顺序能直接到达的点标记辅助数组对于的值1，并且把他们进一个队列中。

用到队列，主要是因为要保证每个遍历的节点先进先出，达到一层层往外扩散的效果，保证标记由近到远。

然后从队列中取出一个点，再按照上下左右顺序遍历，并且判断能遍历到的点对于的辅助数组的值是否为-1，它表示还没有遍历的。如果是 -1 ，将其标记为当前点辅助数组的值加1，并且把点位置进队，不断重复这样的操作。

当判断到遍历到的点为目标点的时候，停止遍历。如果一直到队列为空了的时候，都还没有遍历到目标点，则表示起点到目标点是没有通路的了。

遍历过程图大概如下：

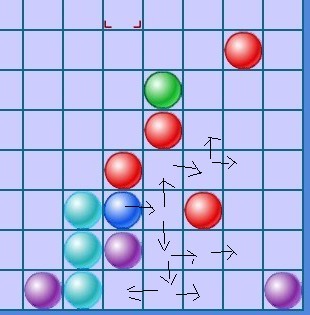
当遍历到2 的时候，辅助数组对应的值大概如下：

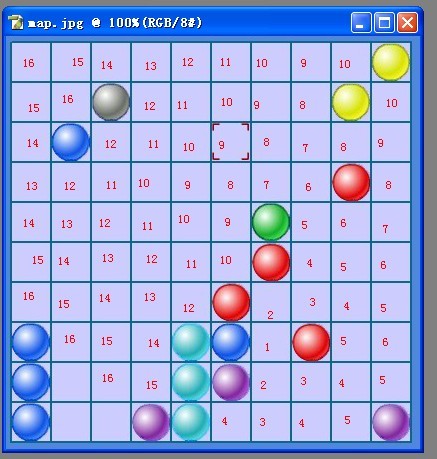
可以看到，当遍历了到第16层（深度）的时候，已经遍历到了目标位置2 处了，没有必要继续遍历了，停止遍历，准备回退查找最短路径。

2 回退

从目标2 开始，按照上下左右的顺序，查找一个比自己小1 的位置（辅助数组里面储存着该值），放到一个数据栈里面。如上图的就是（0,6）入栈，（0,5）入栈，（0，4），（0，3），（1，3），（2，3），（3，3），（4，3），（5，3），（6，3），（7，3），（7，4），（7，5），（7，6），（6，6），（6，7），（5，7）到达起点。根据栈先进后出属性，挨个出栈就是最短路径了

也就是下图的箭头的反方向，就是一个最短路径。

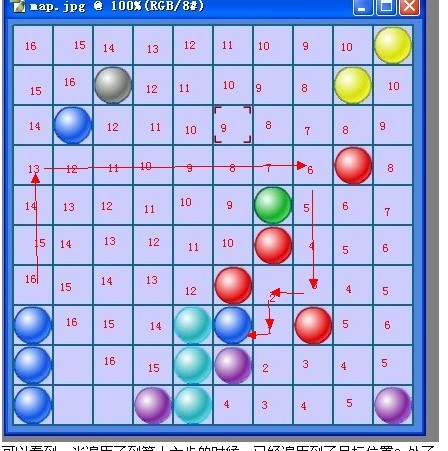
算法基本思想就这样，^_^。

该算法是广度优先遍历，如果地图很大，算法也要借助一个很大的地图，如果距离较远的时候，需要遍历大部分节点，速度不算快。

伪代码：

define SIZE 10

define OUT_OF_MAP(x,y) ((x)<0) || ((y)<0) || ((x)>=SIZE) || ((y)>=SIZE)

struct Point {
    int x;
    int y;
}

// 地图map 中，有珠子的map 的数值非0，空位置的为0
List<Point> search(int map[SIZE][SIZE], Point from, Point to)
{
    int AuxiliaryMap[SIZE][SIZE] = {-1} // 辅助数组的所有所有数值都设置为-1

    Queue<Point> queue  // 点的队列

    // 开始位置设置为0，并且把该点放到队列，准备开始便利
    AuxiliaryMap[from.x][from.y] = 0
    queue.inQueue(from)

    // 点的上下左右四个方向的位置偏移
    Point directions[4] = [{0,1}, {1,0},{-1,0},{0,-1}]

    // 记录是否到达了目标
    found = false

    while (!queue.isEmpty()) {
        Point pos = queue.outQueue()

        // 遍历该点的四个方向
        for direction in directions {
            Point traverse = {pos.x + pos.x, pos.y + pos.y}

            if OUT_OF_MAP(traverse.x, traverse.y) {
                continue // 确保没有越界
            }

            if (map[traverse.x][traverse.y] != 0 && traverse != to) {
                continue // 存在障碍，并且不是目标点
            }

            AuxiliaryMap[traverse.x][traverse.y] = AuxiliaryMap[pos.x][pos.y] + 1
            queue.inQueue(traverse)

            if (traverse == to) {
                // 到达目的地，推出循环即可
                found = true
                break
            }
        }

        if (found) {
            break
        }
    }

    if (!found) {
        // 不是通路，没有可行路径
        return []
    }

    // 存在通路时候，从 to 开始，一步一步找比自己低的点，一直到0，入栈，再把栈的点出栈，就是最近路径了
    Stack<Point> stack  // 用于保存当前路径

    Point traverse = to
    while (true) {
        stack.push(traverse)

        if (AuxiliaryMap[traverse.x][traverse.y] == 0) {
            break // 到达了开始位置
        }

        // 找出旁边比自己小1的那个点
        for direction in directions {
            Point next = {traverse.x + direction.x, traverse.y + direction.y}

            if OUT_OF_MAP(next.x, next.y) {
                continue // 确保没有越界
            }

            if (AuxiliaryMap[traverse.x][traverse.y] == AuxiliaryMap[next.x][next.y] + 1) {
                traverse = next
                break
            }
        }
    }

    List<Point> result
    while (!stack.isEmpty()) {
        result.append(stack.pull())
    }

    return result
}

游戏代码：

https://blog.yuccn.net/wp-content/uploads/2020/11/%E4%BA%94%E5%AD%90%E8%BF%9E%E7%8F%A0_release.rar

（全文完）

（欢迎转载本站文章，但请注明作者和出处 云域 – Yuccn ）