在老刘的知识星球上看到一道有意思的题目，如下：

int HW(unsigned int n){
    n = (n & 0x55555555) + ((n & 0xaaaaaaaa) >> 1);
    n = (n & 0x33333333) + ((n & 0xcccccccc) >> 2);
    n = (n & 0x0f0f0f0f) + ((n & 0xf0f0f0f0) >> 4);
    n = (n & 0x00ff00ff) + ((n & 0xff00ff00) >> 8);
    n = (n & 0x0000ffff) + ((n & 0xffff0000) >> 16);
    return n;
}

提问者提问这个算法是干什么的，评论里面有人给出了答案——判断无符号数二进制写法中有几个1。题目这个算法写得有点悬，拿来分析下，得出下面笔记。

某32位无符号整数n，用二进制写法为：n = xxxxxxxx xxxxxxxx xxxxxxxx xxxxxxxx ，每个x 表示0 或者 1。
把这个xxxxxxxx xxxxxxxx xxxxxxxx xxxxxxxx 每位拆开来写，假定为这样：X0,X1,X2……,X30,X31。
计算其1 的个数，也就是把每个Xk 加起来即可。
count_of_one(n) = X0+X1+X2……+X30+X31
=（X0+X1）+（X2+X3）……+（X30+X31）

由于X0，X1 要么是0 要么是1，所以X0+X1之和 结果小于2（使用二进制写法是10），也就是使用两个bit 就可以保存了。
假设一个数r 是两位bit大小的数字，那么它的二进制1的个数和则是：
(r&0x01) + ((r&0x02)>>1)
如果0x01 和0x02 使用二进制的写法，那么这个数字也就是：
(r&01) + ((r&10)>>1) 写法（1）

这里我们把n的每两个bit 看出一个数字，计算每两个bit 的1个数，存放在原来位置
也就是把X0+X1 的结果，存储在原来数据n 的内存上的bit0，bit1（作为一个内存整体，下称bit[0,1]）上；
把 X2+X3 的结果，存储在原来数据n 的内存的bit[2,3]上；
把 X4+X5 的结果，存储在原来数据n 的内存的bit[4,5]上；
……
把 X30+X31 的结果，存储在原来数据n 的内存上的bit[30,31]上；

按照写法（1）的方式，就是这样了：
n = (n & 01010101 01010101 01010101 01010101) + ((n & 10101010 10101010 10101010 10101010) >> 1)

二进制数字 01010101 01010101 01010101 01010101 的十六进制写法 0x55555555，
二进制数字 10101010 10101010 10101010 10101010 的十六进制写法 0xaaaaaaaa，
采用十六进制的写法，则是：
n = (n & 0x55555555) + ((n & 0xaaaaaaaa) >> 1);

到这里可以看到，（X0+X1），（X2+X3）……，（X30+X31）的数值分别存储在n的 bit[0,1]，bit[1,2]……bit[30,31]了。
我们只需要把bit[0,1] + bit[2,3]+ …… + bit[30,31] 即可，
也就是（bit[0,1] + bit[2,3]）+ (bit[4,5] + bit[6,7]）+…… + （bit[28,329] + bit[30,31]）

到此，我们将bit[0,1,2,3]看成一个数字r，把bit[0,1] + bit[2,3] 结果存储在bit[0,1,2,3] 上，采用二进制的写法就是
r = （r & 0011） + ((r & 1100）>> 2)
同样，n的每4位内的每2位做相同的操作，那么就是：
n = (n & 00110011 00110011 00110011 00110011) + ((n & 11001100 11001100 11001100 11001100) >> 2)
也就是十六进制的写法：
n = (n & 0x33333333) + ((n & 0xcccccccc) >> 2 );

到这，每4个bit 的1 相加，结果存储在了n 的每4个bit 里面了。
同理按照上面的方法处理每8个bit内的每4bit，也就是：
n = (n & 00001111 00001111 00001111 00001111) + ((n & 11110000 11110000 11110000 11110000) >> 4)
也就是：
n = (n & 0x0f0f0f0f) + ((n & 0xf0f0f0f0) >> 4);

再重复上面的类似步骤处理每16bit 内的8bit
n = (n & 00000000 11111111 00000000 11111111) + ((n & 11111111 00000000 11111111 00000000) >> 8)
也就是：
n = (n & 0x00ff00ff) + ((n & 0xff00ff00) >> 8);

继续处理32bit （也就是整体）内的16bit
n = (n & 00000000 00000000 11111111 11111111) + ((n & 11111111 11111111 00000000 00000000 >> 16)
也就是：

n = (n & 0x0000ffff) + ((n & 0xffff0000) >> 16);

整合上面的结果，算法就是这样了：
n = (n & 0x55555555) + ((n & 0xaaaaaaaa) >> 1);
n = (n & 0x33333333) + ((n & 0xcccccccc) >> 2);
n = (n & 0x0f0f0f0f) + ((n & 0xf0f0f0f0) >> 4);
n = (n & 0x00ff00ff) + ((n & 0xff00ff00) >> 8);
n = (n & 0x0000ffff) + ((n & 0xffff0000) >> 16);

综上，思路就是，每相邻两个数值，归并起来，不断重复一直到合成一个。

图解来看就比较清楚了：

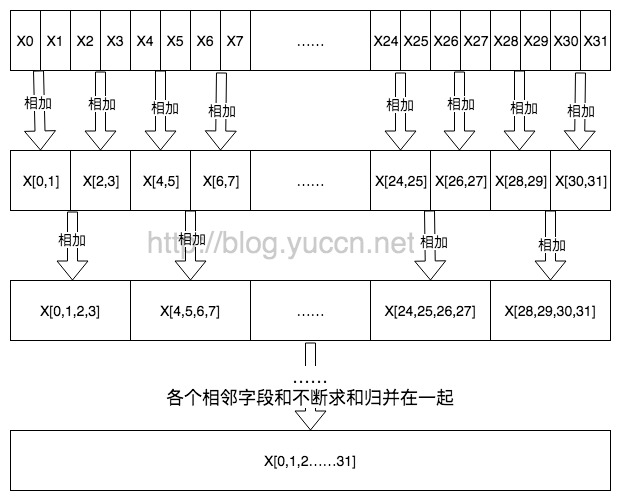
到最后，x[0,1,……31]存储的就是结果了。

（全文完）

（欢迎转载本站文章，但请注明作者和出处 云域 – Yuccn ）