在我们的小学课本中，介绍圆锥体积，用到的是实验的方法，使用锥斗装沙，三次刚刚好将（等底同高）圆柱装满，从而证明它体积是圆柱的1/3。

但我们的教科书没有证明过程，较为可惜了。最近看一本书：《欢乐数学之疯狂微积分》（[美] 本·奥尔林 著），里面介绍了一种方法，非常生动和巧妙，小学生都看得懂的一种方法。

问题特例化

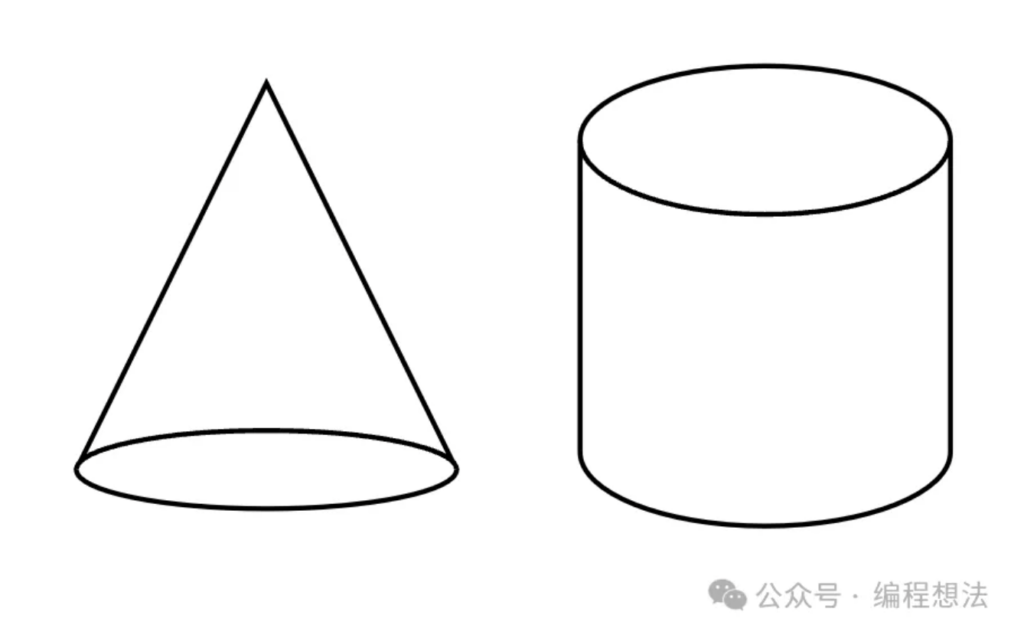
它的论证过程是这样的，将问题特例化：找一个正方体和一个圆柱来做证明。图1如下，右边位正方体；左边是和正方体“等面同高”的圆柱，所以他们两个体积一样。

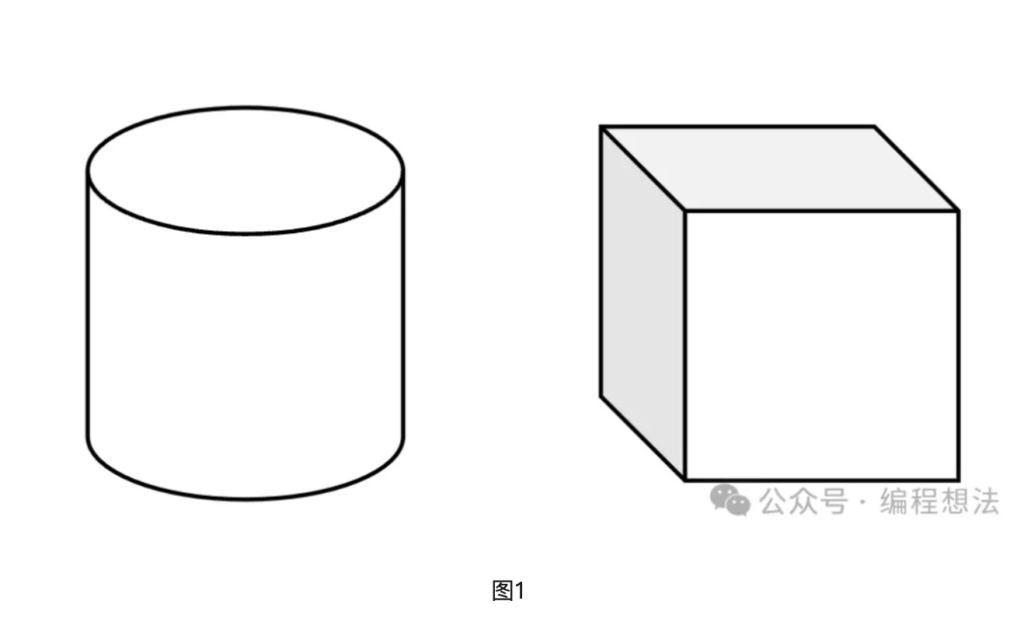
体积关系，即：V(圆柱) = V(正方体) ……（1）。

对应下图2的锥体，左圆锥和（图1）圆柱的底面和高都相等，而右边方锥和（图1）正方体等底同高。

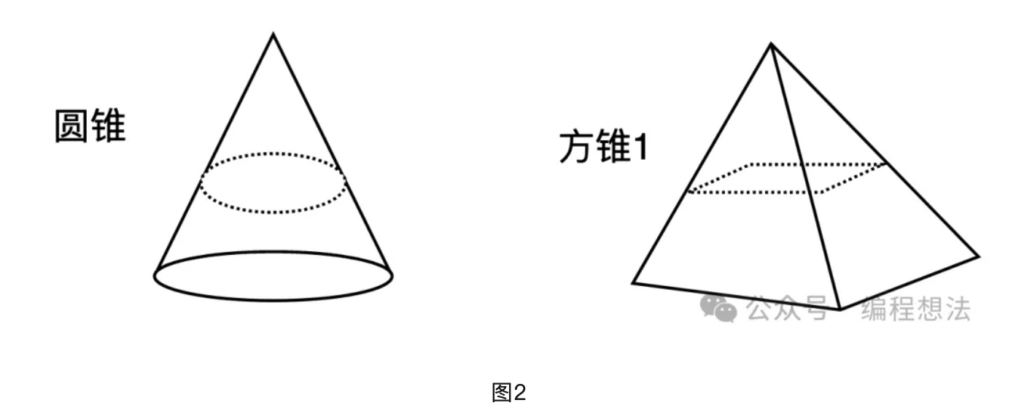
由于相似关系，圆锥和方锥同一高度的截面积是相等的，明显有关系：两个锥体的体积相等。（面积对高度进行积分，就是体积嘛）
体积关系，即：V(圆锥) = V(方锥)……（2）。

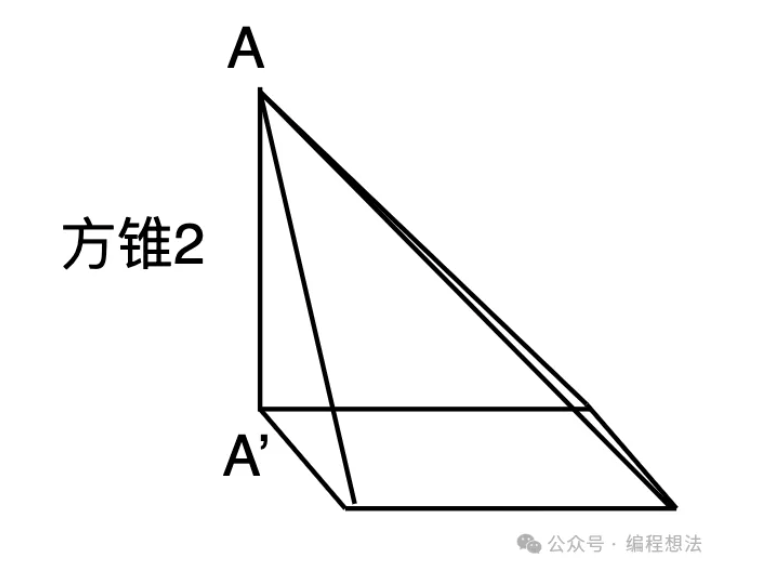
由（1）和（2），只要证明了方锥体积是正方体的1/3，即证明了圆锥体积是圆柱1/3。继续作方锥2，底面和方锥1相等，高也相同，如下图3最右边。注意这个方锥2的一边AA’垂直于底面。

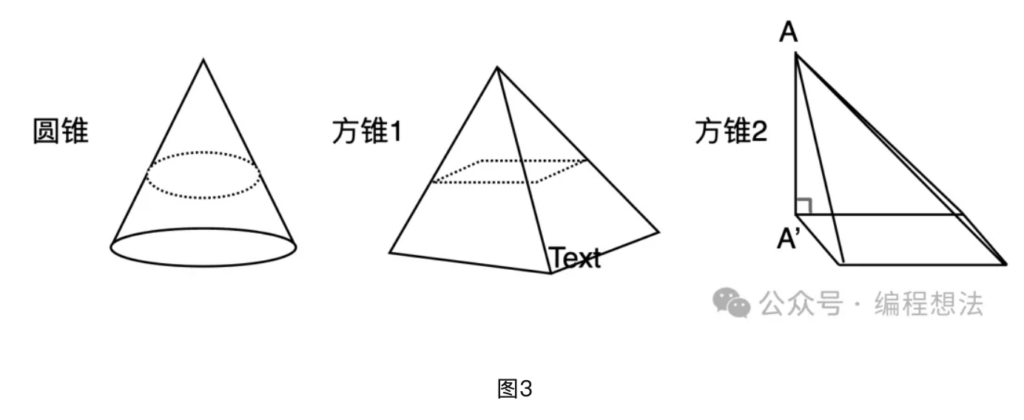
有这三个方锥体积是相等的，即：V(圆锥) = V(方锥1) = V(方锥2)。

所以，只要证明：方锥2的体积，为正方体的1/3便可。

将正方体切开

如下图，我们对正方体进行标记和作辅助线：AB’、AC’、AD’、AC。

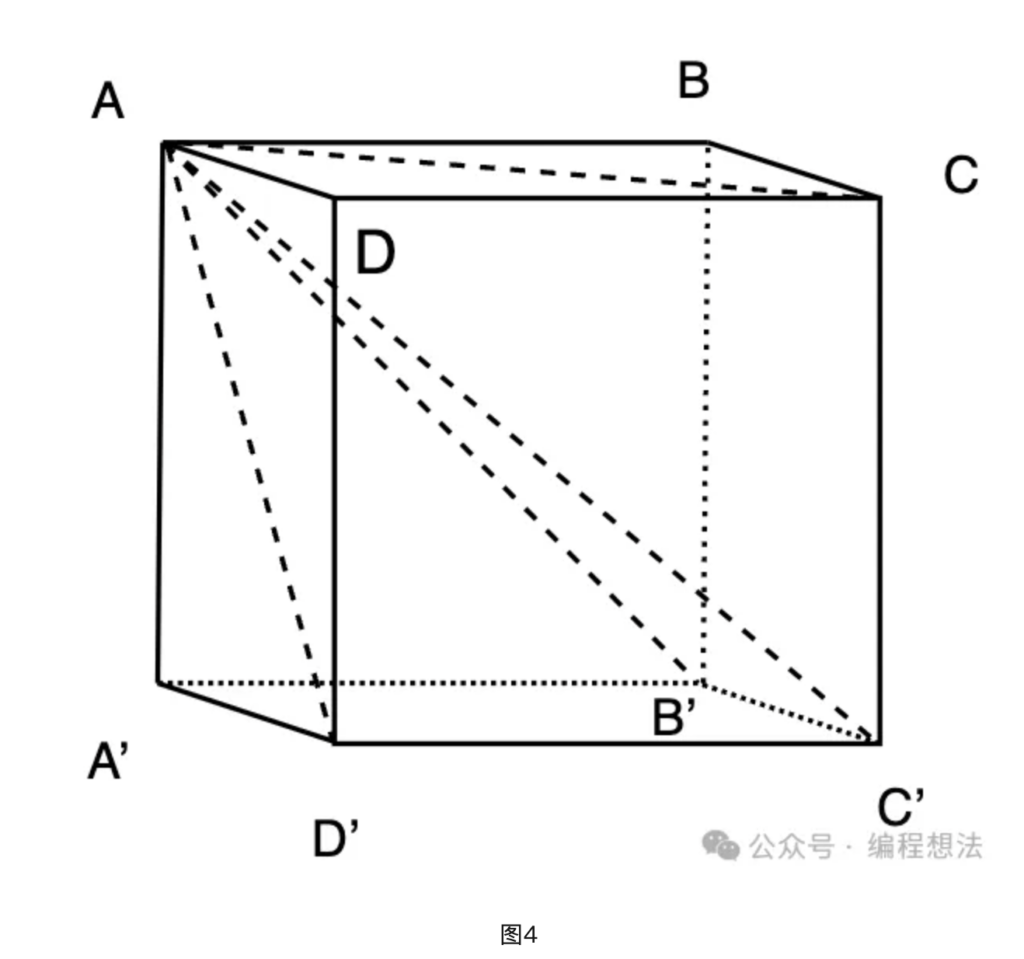
沿着虚线的面将正方体剖开，分成三个多边体：AA’B‘C’D’、ADCC’D’、ABCC’B’，切割开来就是下图这样了：

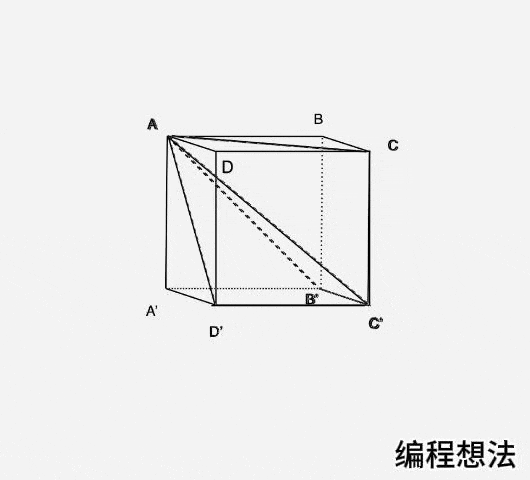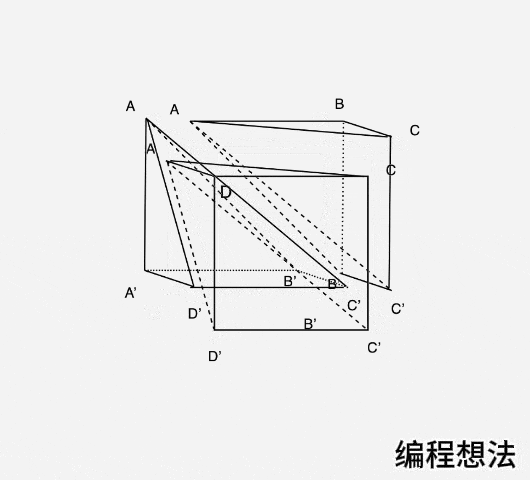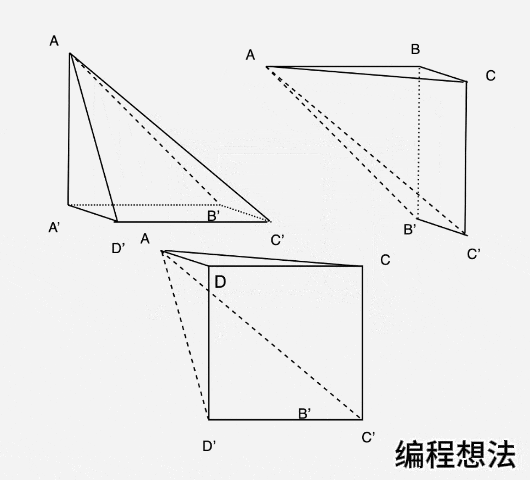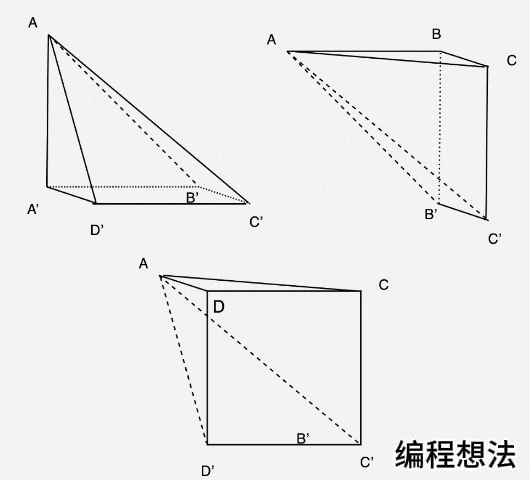
图5

也就是如下图6关系：

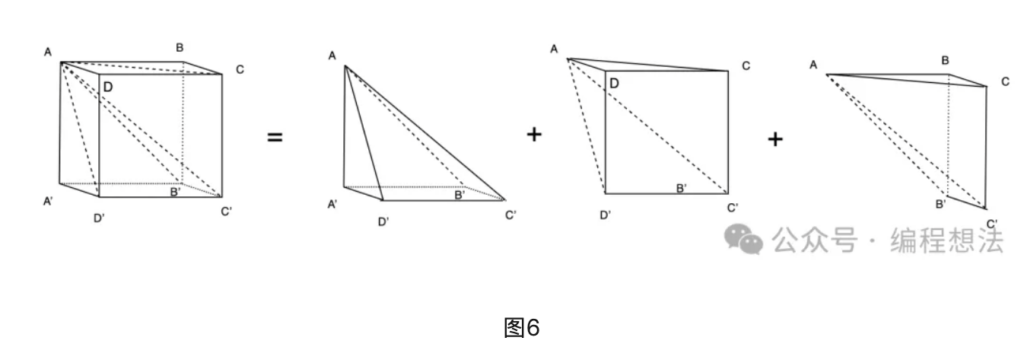
看出啥了不？图6的右边三个多边体，是三个全等的五面体，这三都是锥体2。右边两个，只是摆放方向不一样而已。

既有体积关系：

V(正方体) = V(方锥2) x 3

=> 1/3 V(正方体) = V(方锥2)

=> 1/3 V(圆柱) = V(圆锥)

也就是圆锥体积为圆柱的1/3，证毕。

最后

数学是需要严密的证明的，这个只是证明了“和正方体等面同高”的圆锥，是对应圆柱的1/3，只是证明了特例，还没有推证到所有情况，所以这个证明是不充分了。但作为一个趣味学习，这个证明的思路，是比较有意思的。

（全文完）

（欢迎转载本站文章，但请注明作者和出处 云域 – Yuccn ）