一文弄懂动态规划,从递归公式到动态规划
动态规划,作为算法中比较实用用和好玩的一种,却常常给人一种神秘的面纱。
如果将其拆解,抽丝剥茧,会发现其有着通用的共识和套路,竟然是如此简单。
本文从简单开始,慢慢图解动态规划的那些套路。
从递归开始
学过编程的朋友应该都理解递归,按理不用多讲述,但是还是从它开始吧,从基本的开始:要计算从1到100,作为头脑的预热。
最直接想到的是一个for 循环挨个加就可,要啥递归?
但就是要用递归去做呢?
要计算sum(100),则先计算sum(99),再加上100就可;
要计算sum(99)?那就sum(98),再加上99;
……
要计算sum(1)?它是最后一个了,直接return 1 即可。
# 从1到 N 的正数和
def SUM(n):
if n <= 1:
return n
front = SUM(n-1)
result = front + n
return result实际写代码肯定不会如上面那样写(一个迭代能搞定谁用递归?)。
只是想表达一个基本的的思路:处理一个大问题时候,拆分为小问题处理,再把子问题结果做整合,作为本问题结果,使得问题更简化。
我们可以清晰得到,递归的基本结构:
递归的基本结构:
1 结束条件处理;
2 子问题处理;
3 本层问题处理;
4 整合结果,返回。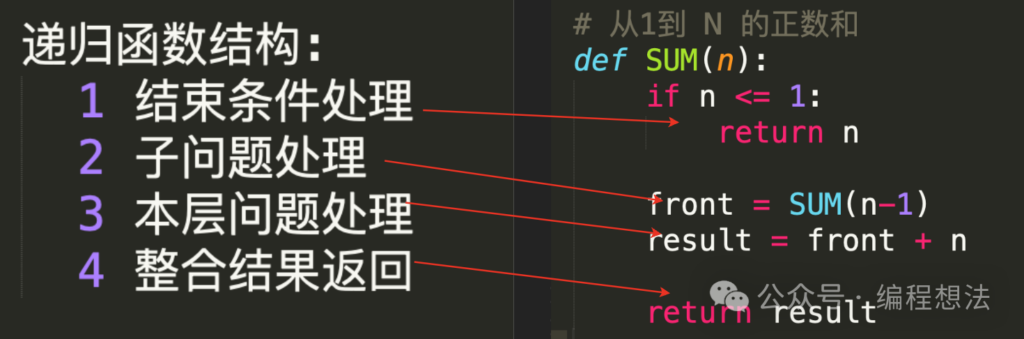
好了弄懂递归问题了,那么动态规划问题就了解一半了,喝口茶休息下~
别急,我们继续慢慢看。
动态规划的结构
用递归来做动规,动态规划的结构,并没有比递归复杂太多,他们有着接近的结构(注:动规也可以不用递归来弄,用迭代也行,不讨论这个情况了),我们可以整理动态规划的简约公式:
动态规划 = 递归 + 存储化记忆
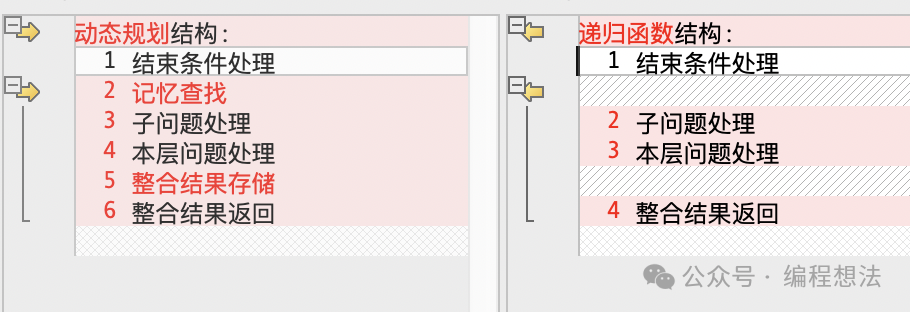
直接上动态规划的结构吧:
动态规划结构:
1 结束条件处理
2 记忆查找
3 子问题处理
4 本层问题处理
5 整合结果存储
6 整合结果返回动态规划比递归多了2和5,也就是存储化记忆部分。
稍微复杂点的是,动态规划的子问题不会像递归那么直接,它可能有多个子问题要处理,所以在整合结果时候也会复杂一点点。
动态规划例子
直接看一个实际例子——莱文斯坦距离计算:
莱文斯坦距离:由一个字符串转成另一个字符串所需的最少编辑操作次数,编辑一次包括删除一个字符、插入一个字符、替换一个字符三种。莱文斯坦距离也是计算两个字符串的相似度问题。
比如:”abcd” 要转为”abc”,莱文斯坦距离为1,也就是把后面d删除,一次操作;
再比如:”abcd” 要转为”aked”,莱文斯坦距离距离为2,b替换为k,c替换为e,两次操作。
动态规划,通常都有一个递推(倒推)的过程,一般称为状态转移。把当前问题求解,拆分为一个或者几个子问题求解,再做整合。莱文斯坦距离问题,也是如此。
(为了讲述方便,先约定下,大写S[n] 表示长度为n 的字符串S,小写s[n] 表示S的第n个字母)。
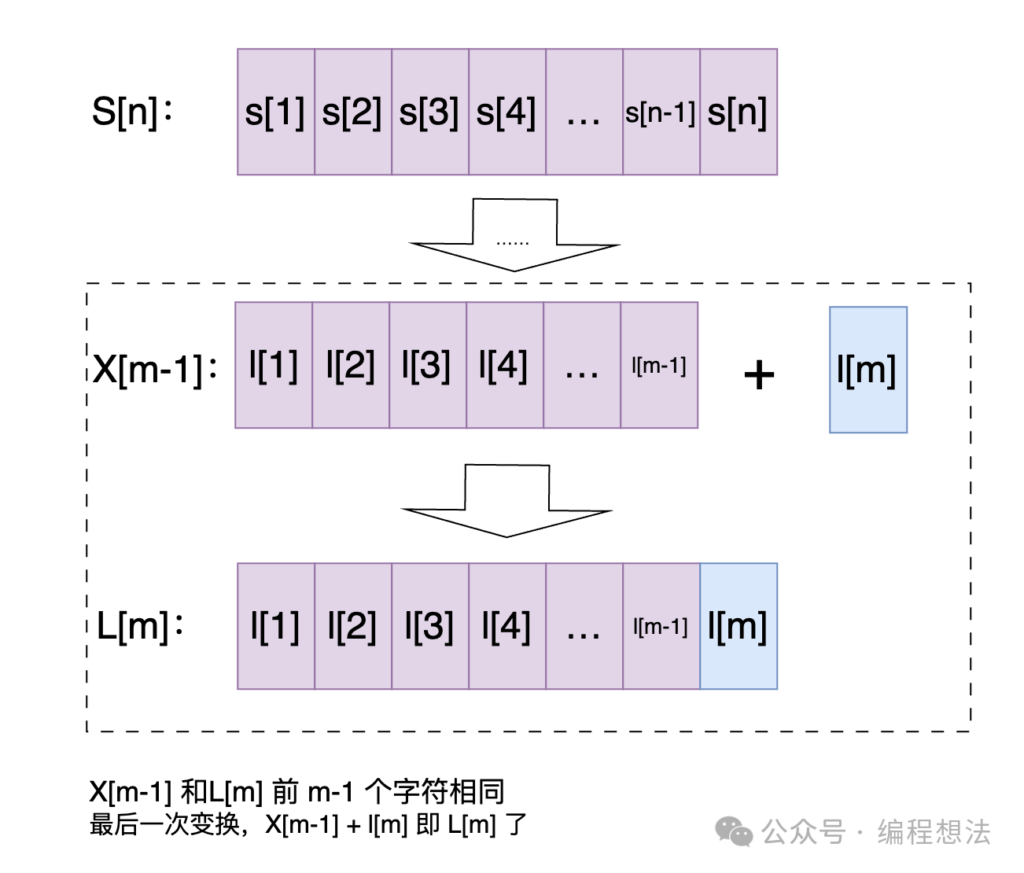
长度为n的字符串S[n],转为长度为m的字符串L[m]。
我们假定最后一次转换是最后一个字母,则最后一次转换,不外乎是下面几种情况(子问题拆分):
1) S[n]转为某个字符串X[m-1](X和L的前m-1个字符相同),之后增加一个字符;
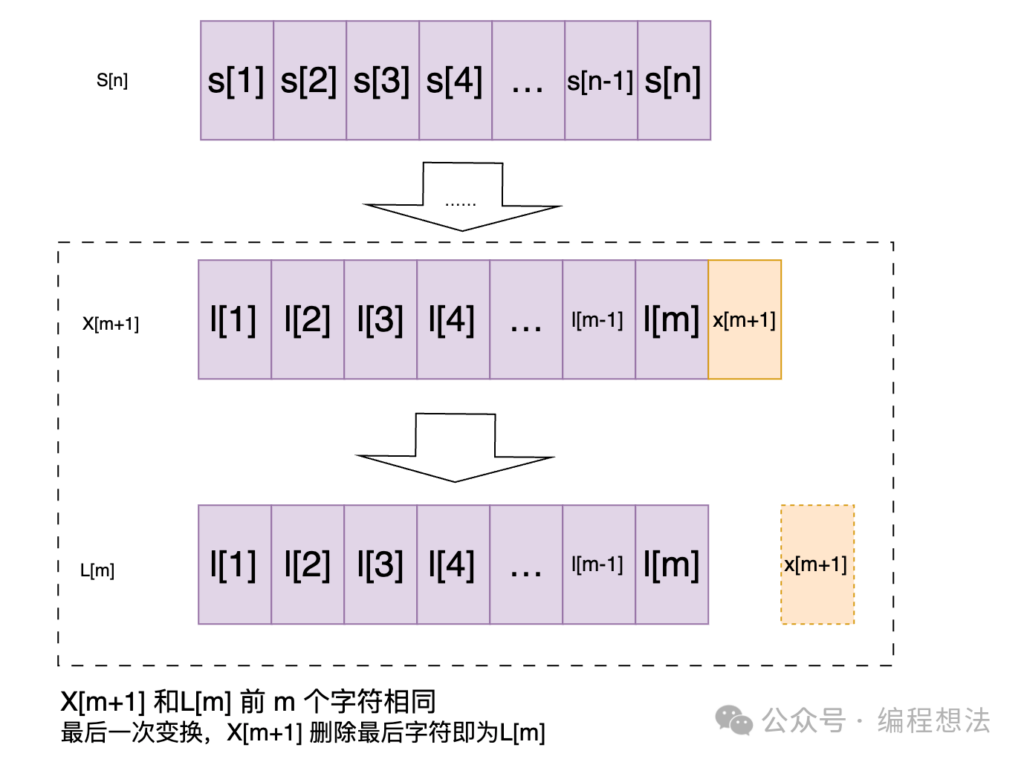
2) S[n]转为某个字符串X[m+1](X和L的前m个字符相同),之后删除最后一个字符;
3) S[n] 转为某个字符串X[m](X和L的前m-1个字符相同),修改最后一个字符;
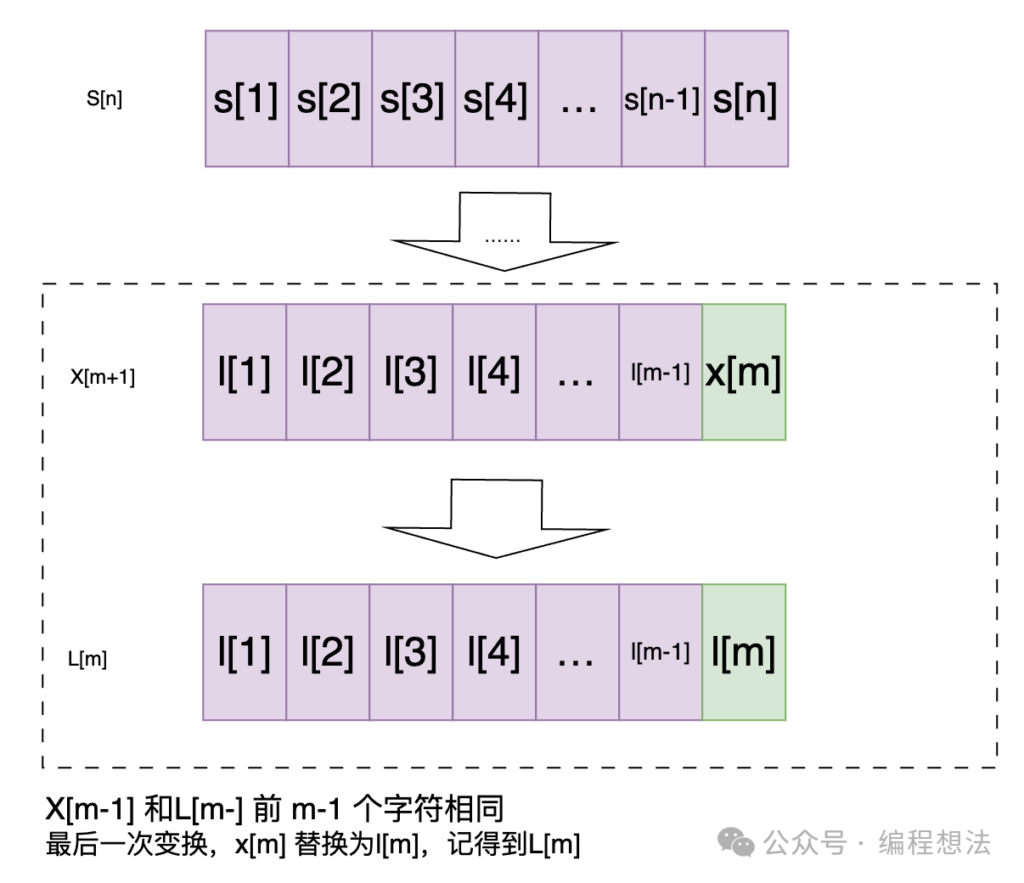
上面说的变换是在最后一个字符的情况,但如果最短距离变化的不是在最后一个字符,而是在中间呢?
好问题,再认真分析,发现这种情况,囊括在情况3了,差异在于x[m]和l[m] 两个字母也相等,即最后一个编辑次数为0就等价了。
代码部分
用func = dp(s1, s2) 表示莱文斯坦距离(LevenshteinDistcance) 。
S到L如果是从情况1过来的,则LevenshteinDistcance 为:
distcance1 = dp(s1, s2[:-1]) + 1
# 等价 dp(s1, s2[:-1]) + dp("", s2[-1])如果是从情况2过来的,则LevenshteinDistcance 为:
distcance2 = dp(s1[:-1], s2) + 1
# 等价 dp(s1[:-1], s2) + dp(s1[-1], "")
如果是从情况3过来的,则LevenshteinDistcance 为:
distcance3 = dp(s1[:-1], s2[:-1])
if s1[-1] != s2[-1]:
# 最后一个字符不同,才需要增加距离
distcance3 += 1
# distcance3 = dp(s1[:-1], s2[:-1]) + dp(s1[-1], s2[-1])(三个路径过来)三者取最小值,则是S到L的莱文斯坦距离了。
所以,整理代码有:
def dp(s1, s2):
if s1 == s2:
# 字符串相等,距离0
return 0
if s1 == "" or s2 == "":
# 某个字符串为空,变化就等于非空的字符串长度了
return len(s1) + len(s2)
if len(s1) == 1 and len(s2) == 1:
return 1 # 替换
distcance1 = dp(s1, s2[:-1]) + 1
# 等价 dp(s1, s2[:-1]) + dp("", s2[-1])
distcance2 = dp(s1[:-1], s2) + 1
# 等价 dp(s1[:-1], s2) + dp(s1[-1], "")
distcance3 = dp(s1[:-1], s2[:-1])
if s1[-1] != s2[-1]:
# 最后一个字符不同,才需要增加距离
distcance3 += 1
# distcance3 = dp(s1[:-1], s2[:-1]) + dp(s1[-1], s2[-1])
distcance = min(distcance1, distcance2, distcance3)
return distcance
就酱紫?我们运行下,看看连云港(lianyungang)到石家庄(shijiazhuang)的莱文斯距离:

那么短的字符计算,运行时间17秒+,这性能接受不了吧。而且字符每长一个字符,运行时间指数增加。
等等,上面的代码,仅是递归而已,还不是动态规划,仅有动态,没有规划啊!
就好比你点个剁椒鱼头,结果上来一个清水鱼头没有剁椒,甚至上来是一碟剁椒没有鱼头,你抓狂不?
前面说过:
动态规划 = 递归 + 存储记忆。
说好的存储化记忆呢?

现在就加上。
由于计算dp(s1, s2)时候,有大量s1的子字符转换为s2的子字符的重复计算,重复计算都是被浪费掉的。
我们做个缓存,在计算前,先在缓存查找,有则返回,没有则计算,再存储后返回。
再整理的完整代码(比上面的,多了红色部分):
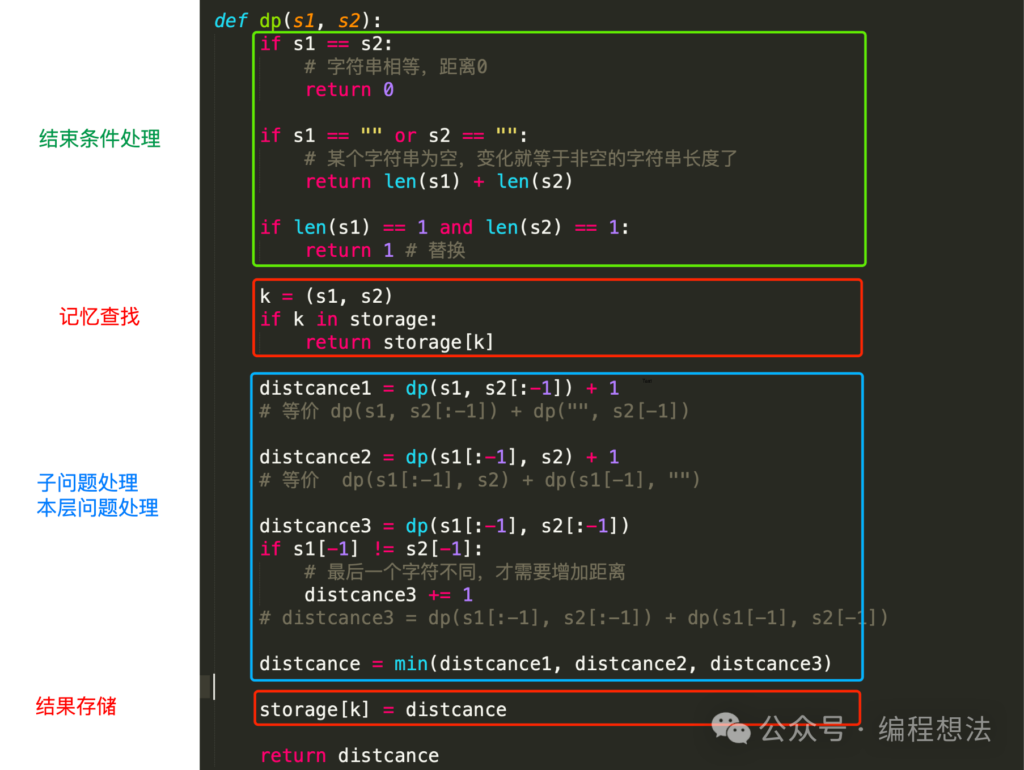
上述代码定义了scores = {}作为缓存,利用python的tuple(元组)可以作为key 的特点,直接用(s1,s2) 作为scores的key,就省去了定义复杂的缓存设计了。
加上存储记忆之后,运行情况:

总结
动态规划 = 递归 + 存储记忆。#(第三次出现了)
做动态规划的过程,都可以写下面的函数框架(俗称自上而下编程),之后每个分支填上对应的代码就可。

动规最考头脑的部分在于子问题的拆分,不同问题有不同的分析,这个就看实际情况而定了。
相应的leetcode有(一次编辑问题):https://leetcode.cn/problems/one-away-lcci/description/
其实就是判断其距离是否超过1。
(全文完)
(欢迎转载本站文章,但请注明作者和出处 编程想法 – Yuccn )