异或（xor）逻辑运算的基本操作，也计算机领域特别密码学应用的基础，其运算规则：

用语言描述，可以简化为“两bit 相同，则0；两bit不相则1”。

就算这样简化的一个逻辑，对于部分女生来说，说不定还是不好理解。为什么异或两次等于本身？就更难解析了。

《无处不在的算法》一书，《最简单最安全的保密方式》篇，有一例子，用硬币的“翻转”操作做比拟，这是对“异或”最生活化的一个解析了。

硬币表示

如果有两块硬币，一块正面朝上，一块反面朝上，如下：

上面的硬币为：（正面，反面），数据化就是(1,0)。

如果要对上面两块硬币进行操作，第一块翻转，第二块不变，也就是操作：（翻转，不翻转）

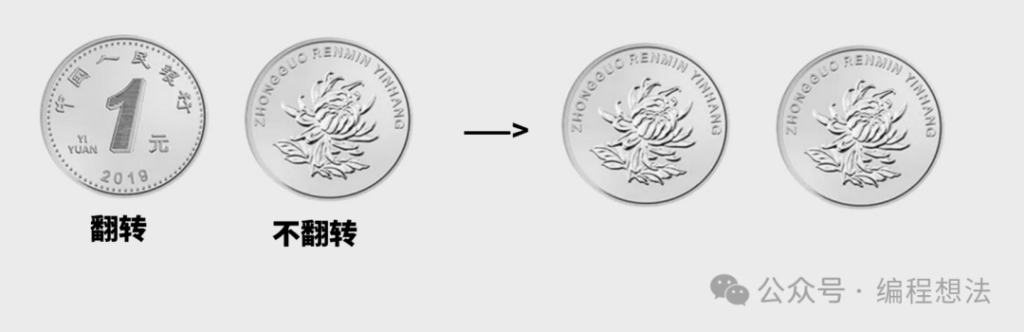
硬币（正面，反面） + 操作（翻转，不翻转） = 硬币（反面，反面）。

把“翻转”用1表示，“不翻转”用0表示，再把它们的组合表示出来，“硬币的翻转”情况，就是异或运算过程；或者异或运算，就是“硬币的翻转”过程。

八块硬币操作

为什么特别说8块？因为8bit 就是一个字节嘛。

如果有八个硬币情况：（正面，反面，反面，正面，正面，正面，反面，正面）；

他们分别操作（翻转，不翻转，翻转，不翻转，翻转，不翻转，翻转，不翻转）。

也就是这样的操作：

硬币(1,0,0,1,1,1,0,1) + 操作（1,0,1,0,1,0,1,0）= 硬币(0,0,1,1,0,1,1,1)。

这就是一个字节数据和另一字节数据的异或过程。

bit(10011101) xor bit(10101010) = bit(00110111)，也就是 157 ^ 170 = 55。

为什么对一个数字进行异或两次，等于本身？

看下图，就再清晰不过了：

我们把“翻转”的操作(也就是操作bit为1部分)，用红框框出来；“不翻转”的无视。这或异运算两次，就是特定位的硬币翻转两次。

没框部分，“不翻转”两次，数据没变；红框部分，翻转两次，也等于本身。

特定位的硬币翻转两次，得到的数据肯定等于原来的数据啦！

（全文完）

（欢迎转载本站文章，但请注明作者和出处 云域 – Yuccn ）