在讨论比特币时候，技术上讨论最多的就是区块链。在介绍区块链之前，先从挖矿说起。

1 矿机、挖矿什么、矿池又是什么

比特币交易的数据是分布式存储记录的，在《认识比特币（2）——比特币诞生故事》文章里面提到需要找一干人来记账，挖矿本质就是记账，把一段时间内的交易打包在一起（一个区块），从而获得报酬——比特币，这个打包过程就是“挖矿”了。

直接地理解：矿机就是在不停的“挖矿”的机器（电脑），一堆矿机组织起来一起“挖矿”，平分一起挖到的“矿”，这堆机器就是一个矿池了。

2 挖矿的报酬来自哪里

作为报酬的这些比特币如何来？主要来源有两个。

1）系统生成。《认识比特币（3）——比特币上限为什么是2100万》提到，每生成一个区块就会按照约定生成一定的比特币奖励给矿工。但按照比特币“发行”约定，这个生成的比特币会越来越少的，总有一天生成的比特币会变成零。

2）交易手续费。在比特币交易中，可以拿出一点费用作为手续费，付出手续费的交易会优先被矿机记录，这样才能使得有矿机们继续工作（记账）下去——没有利益的劳动，谁会做？在比特币“发行”完毕后，矿机的主要报酬就是来自这部分了。

3 区块和区块链简说

挖矿表面就是上面那些了，本质上就是记账，把一堆账目（交易）打包在一起，就是一个区块。区块里面有很多交易条目，同时它也带有其他一些数据，比如hash、时间戳、索引号、上一块数据hash、随机数等。很多区块一个一个有机组织在一起，就是一条区块链了。

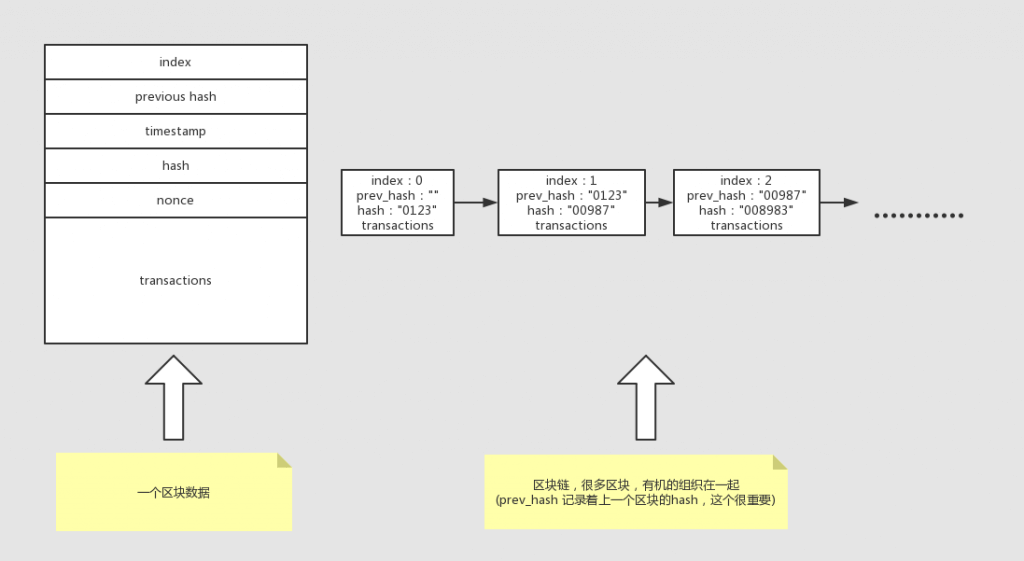
上图，左边就是一个区块的示意图（实际上还有其他数据），右边就是区块链示意。区块链内的区块是有机关联着的，除了第一个区块（创世块）外，每个区块都记录着自己的hash值和上一个区块的hash值。如上图块2的prev_hash 就是块1的hash，块3的prev_hash就是块2的hash。

4 谁来记账区块——工作量证明

如果只是把交易简单的组织在一起，是非常容易的事情，任何一个矿机都可以轻松完成。大家都可以轻松打包记录的事情，作为奖励的报酬给谁？这里就得来个“裁判”了，这里的“裁判”就是工作量证明（Proof Of Work，简称POW）——大家来算一条数学题吧，谁先算出，打包权和奖励金归谁。

每个区块里面有个记录信息摘要值 hash（简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数，下说哈希值）和随机数nonce，工作量证明就是在这个哈希值和nonce做文章了。

这道“数学题”是这样的：计算的哈希值有个这样要求，算出一个nonce，使得整个区块的哈希值前面有n个0（n称为计算难度）。哪个矿机先计算出合要求的nonce 和哈希，它就获得这次的记账权和奖励，同时把结果广播给其他矿机。

其他矿机收到有矿机计算好了的区块数据，则停止本轮争夺记账，马上进行下一轮记账权争夺。

做个比喻，如果数据为”hello china.”，而计算难度要求为3，要求算一个n，使得 “hello china.n” 的哈希值格式为：“000xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx”，也就是前面三个要求为0。跑测试得:

sha256("hello china.0") = "72442cbab482ac912ab04a4d735ca13afad5d47970649fd4683775cb6080cd4f"
sha256("hello china.1") = "25d64131521b3c83d27c3cae53ef79e573bc27e3658566c25c33bffe8ba588a7"
sha256("hello china.2") = "bc79953d627fc9de365ed26018d663bafdf8c6c02e236d11816f94eecb484b0f"
……
sha256("hello china.2346") = "000b6d006b4e31d9837f446dca65ebfb7246196cb00e6ee404cf243e73eef413"

也就是nonce=2346满足了要求。如果n较大，这个求值计算量是非常庞大的。

来做个实验，模拟几个数据来创建几个区块，假定三条数据分别是：”zhang san send 10$ to lisi.”、”lisi send 0.01$ to wangwu.”、”wangwu send 100$ to zhaoliu.”。尝试从第一块区块（创世块）开始，创建三个区块，把他们连起来组成一个简单的区块链，第一个区块难度n为3，后面每个区块难度+1。实验打印下数据和运算时间，实验结果如下（代码文章在后面）：

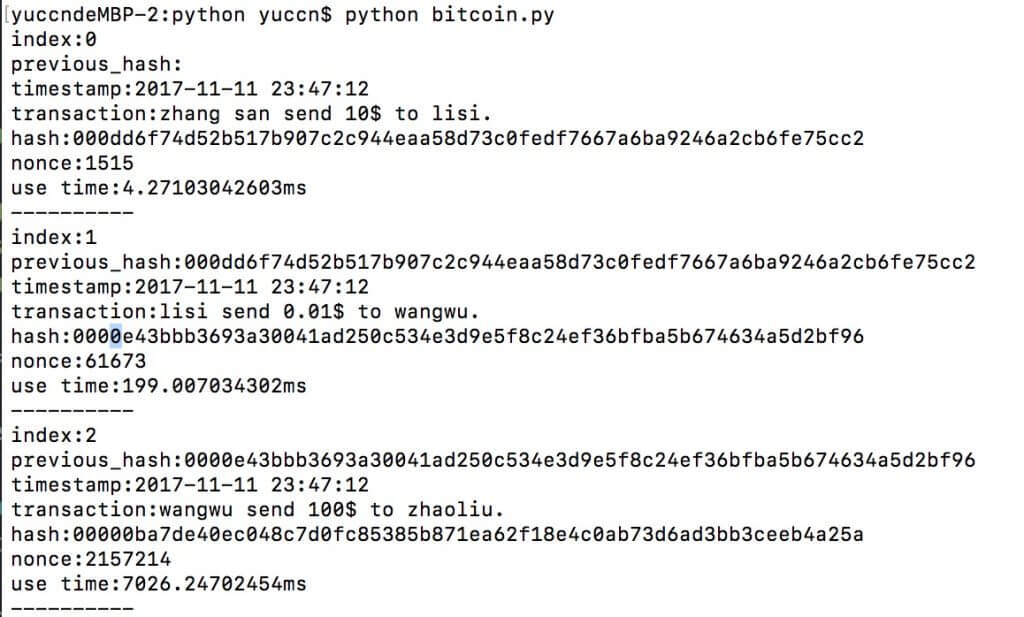
做一个假设：难度为1称为P1，难度为2称为P2……难度为n称为Pn。

上图可知，P3的运算时间（use time）约4.27毫秒，P4的时间约200毫秒，P5的时间约为7026毫秒。可见难度每增加1，计算量会增加一个数量级。哈希值是16进制格式输出（0-f），可以理解计算的某位哈希值是随机的，每位随机就有16种可能了，也就是说难度每增加1，计算量大约会放大16倍。粗略估算P6的计算时间约 7 * 16 = 112 （秒）了。

看一个真实的区块 #494016，其哈希值为：00000000000000000092df3f0a9ca450140ce64f6d196b06767fb89ae543df0d，前面18个0，难度是P18。简单运算下，P18运算量 是P6的运算量的16^12（281474976710656）倍，也就是112秒的281474976710656倍（这是多少年了）。

肯定不能112秒的281474976710656倍时间 来记录一个区块，这里是粗略说“单台机器的112秒的281474976710656倍工作量”。全世界矿机有多少具体不得知道，这些工作量会分摊到全世界矿机去，比特币系统会控制难度，使得大概每10分钟就有一个区块产生。由于有新矿机加入计算也有退出计算，机器硬件和运算速度也在发展，所以矿机们的总算力是在变化的。如果产出区块过快了，系统会控制难度增加，如果产出区块过慢了，难度会减小，使得产出区块在时间上是大约平均的。

矿机算这道数学题如此费力，争夺算出这道题，就是它的工作量证明。矿机耗电耗资源，原因就是耗在这些看似无用的（实质上也没有很大作用）蛮力计算上了。

5 协作挖坑——矿池的出现

矿机算力有强有弱，如果硬件太弱的机器去和强的机器争夺计算，几乎是拼不过的。再如上面估算，单台计算机计算难度为18的区块哈希，时间可能是112秒的281474976710656倍，这是多少年？这样，普通人几乎没有玩（参与挖矿）的可能。但是如果组织100个或者1000个或者10000个矿机在一起合作计算，得到报酬平分，这样就能大大降低了参与挖坑的门槛。这些组织在一起挖矿的机器群，就是一个矿池了。 矿池出现的原因——算力需求太大了。

6 区块链的难修改性

区块链中有个数据——previous hash，这个节点也很重要，它确保了整条链的难修改性。比如，有人恶意修改了第一个区块的数据，那么第一个区块的hash必然变化了，由于第二个区块的previous hash节点数据保存着第一个区块的hash，也就是修改了第一个区块数据的时候，也得修改第二个区块的previous hash才能确保链的完整性，如果修改了第二个区块的previous hash，导致第二个区块的hash 又变化了，还得修改第三个区块的previous hash……如此往复。若修改了某个区块的数据就得修改这个区块之后的所有区块才能确保区块链的完整性——一动则动全身了。这样保障了区块链的不容易被破坏性。

7 实验代码

#-*- coding: UTF-8 -*-
import random
import hashlib
import time

'''
---------------------
[  index            ]
---------------------
[  previous hash    ]
---------------------
[  timestamp        ]
---------------------
[  data             ]
---------------------
[  hash             ]
---------------------
[  nonce            ]
---------------------
'''

def hash_sha256(input):
    sha256obj = hashlib.sha256()
    sha256obj.update(input)

    return sha256obj.hexdigest()


def is_valid_hash_diffculty(hash, difficulty):
    for i in range(0, difficulty):
        if hash[i] != '0':
            return False

    return True


def calculate(index, previous_hash, timestamp, transaction, difficulty):
    hash = ""
    nonce = 0
    while True:
        data = str(index) + previous_hash + timestamp + transaction + str(nonce)
        hash = hash_sha256(data)
        if is_valid_hash_diffculty(hash, difficulty):
            return hash, nonce

        nonce += 1


def print_blockchain(index, previous_hash, timestamp, transaction, hash, nonce):
    print("index:" + str(index))
    print("previous_hash:" + previous_hash)
    print("timestamp:" + timestamp)
    print("transaction:" + transaction)
    print("hash:" + hash)
    print("nonce:" + str(nonce))


if __name__ == "__main__":

    datas = ["zhang san send 10$ to lisi.",
            "lisi send 0.01$ to wangwu.",
            "wangwu send 100$ to zhaoliu."]

    previous_hash = ""

    now = time.time()

    for index in range(0, len(datas)):
         data = datas[index]
         timestamp = time.strftime('%Y-%m-%d %H:%M:%S',time.localtime(now))
         hash, nonce = calculate(index, previous_hash, timestamp, data, 3 + index)
         print_blockchain(index, previous_hash, timestamp, data, hash, nonce)
         previous_hash = hash

         print("use time:" + str((time.time() - now) * 1000) + "ms")
         print("----------")

         now = time.time()

（全文完）

（欢迎转载本站文章，但请注明作者和出处 云域 – Yuccn ）